Venn Diagram Of Quadrilaterals
Venn Diagram Of Quadrilaterals – None of my new potatoes were cooked. All my potatoes are fine to eat in this dish. None of my baked potatoes are edible.
It is a well-known fact that all squares are rectangles, but not all rectangles are squares. We can express these statements as follows.
Venn Diagram Of Quadrilaterals

You have seen Venn diagrams at some point in your life. They are very useful when thinking about logic. For example, “All businessmen are smart” (or “If a person is a businessman, he is smart”) can be represented by the following diagram:
Unit 9 Lesson 2 Quadrilaterals
In this example, Algernon is a shrewd merchant, Aberforce is shrewd but not a merchant, and Aloysius is neither shrewd nor a merchant.

Do the diagrams make it clear that the statements “all traders are wise” and “all wise men are traders” have different meanings?
You’ve seen that if/then statements contain dialog. There are two types of statements you can derive from an if/then statement.

Venn Diagram Worksheet 4th Grade
Select three “test” statements of the form “$A$ if $B$”. When the original statement is present, use them to determine whether the inverse and/or negation must be true. If you’re not sure, try drawing a Venn diagram.
Some of the statements in your list of theorems and theorems can also be written in if/then form and need to be checked to see if they are true. For example, you might have the following statement:

If you’re going to demonstrate dialogue, what’s a given? What will be the effect of what you are trying to prove?
Solved:use The Venn Diagram To Determine Whether Each Statement Is Always, Sometimes, Or Never True. A Rhombus Is A Rectangle But Not A Square. (image Can’t Copy)
Go ahead and prove the statement “If two pairs of opposite sides of a quadrilateral are congruent, then it is a parallelogram.” (Hint: Adding something extra to the picture is a useful problem.)

Another way of saying what you just proved is that two pairs of opposites are congruent
A quadrilateral must be a parallelogram. In other words, if you have a quadrilateral and you know that its opposite sides are congruent, that’s enough—you don’t need to know anything else about it to know that it’s a parallelogram.

Question Video: Finding The Intersection Of Given Sets Using Venn Diagrams
On the other hand, the original statement in your list, “Opposite sides of a parallelogram are congruent”, provides a statement that is true for all parallelograms. Such statement is a
Position because if you have a quadrilateral with no congruent opposite sides, you know you definitely don’t have a parallelogram. You are missing one of the important criteria.

Conditions are always necessary and not desirable. For example, a quadrilateral must have four right angles to be square, but it is not enough for a quadrilateral to have four right angles. A quadrilateral can be a rectangle and still have four right angles.
Resourceaholic: Venn Activities
Also, conditions may be sufficient without being necessary. For example, a closed shape with three 60-degree angles is sufficient to be a triangle, but it is certainly not necessary for a triangle to have three 60-degree angles.

And what’s more, need and want conditions should not be about quantities. For example, at Park, playing football all four years is enough to satisfy your athletic need. Also, one must be a senior to take a senior studio – one cannot take a senior studio without being a senior.
Are park students required to play four years of football to fulfill their athletic requirement? Is being a senior in the park enough to get a senior studio?

Standard G 4 Lesson 6 5 Objectives: 1. Review Of Lessons 6 1, Ppt Download
Poet Lee-Young Lee says, “Every wise child is a sad child.” According to him, is a smart child enough to be a sad child?
Can a number divisible by 8 be divisible by 108? 6 through? By 54?

You organize your little sister’s blocks. In doing so, you create the following Venn diagram to categorize them. State whether each statement is true.
How Can I Use A Venn Diagram To Help Me Classify Plane Shapes?
Your sister’s three blocks are shown in the Venn diagram. Describe each block according to the properties described in the figure.
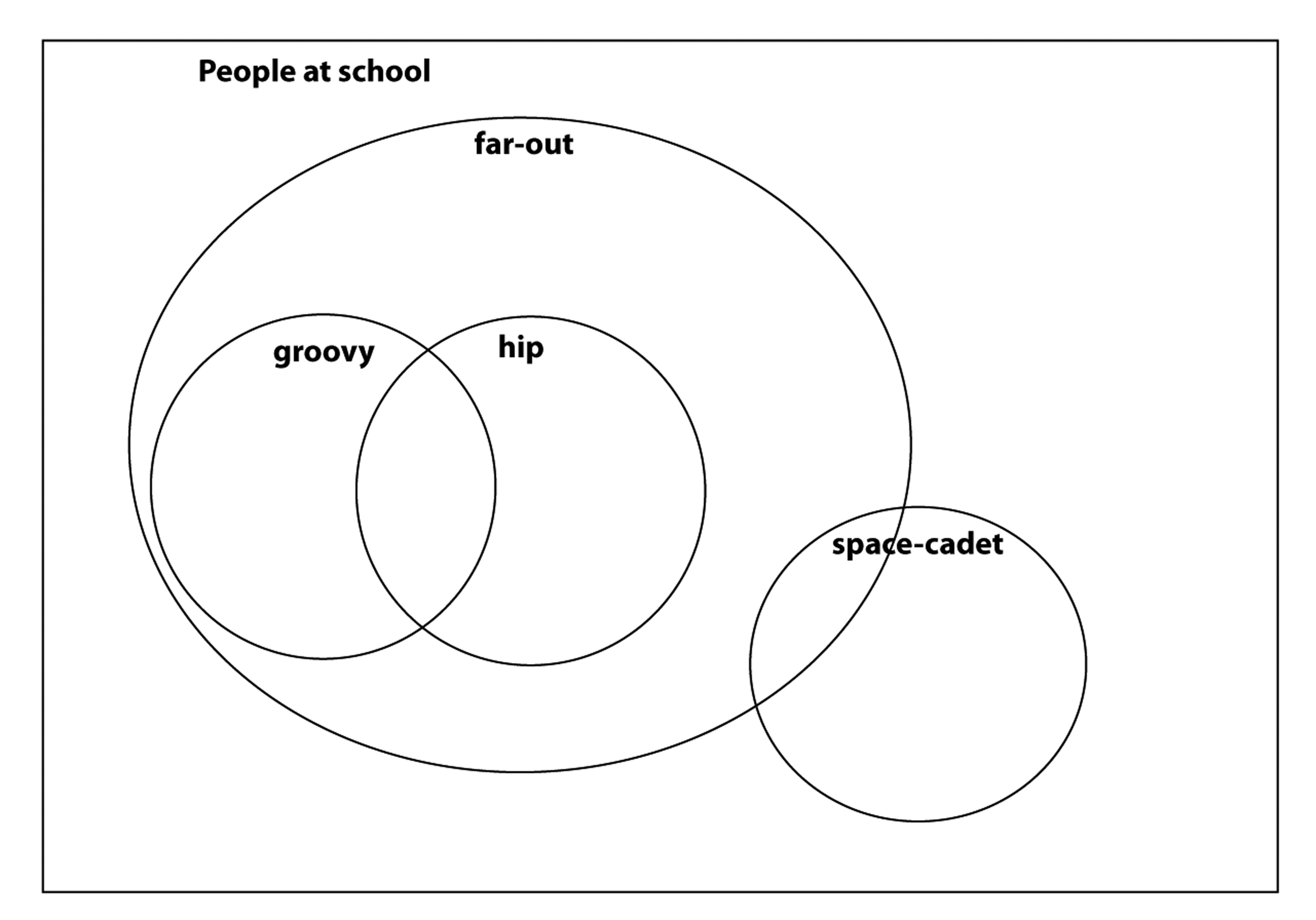
Draw a diagram (perhaps a Venn diagram or “tree” diagram) that clearly shows which quadrilaterals are types of other quadrilaterals (for example, a square is a type of rectangle).
Draw a Venn diagram and use it to see what conclusions you can draw from the Lewis Carroll puzzle below.

Solved: Venn Diagram With Quadrilaterals Place The Names Of The Quadrilaterals In The Correct Place In The Venn Diagram Isosceles Trapezoid Parallelogram Trapezoid Rectangle Square Quadrilateral Rhombus
The statement “No circle is a parallelogram” cannot be represented in a Venn diagram as a circle within a circle.
In the previous lesson you proved that if a circle has two central angles of the same measure, the corresponding chords are congruent.
In the previous lesson you proved that if you draw a line through the center of a circle perpendicular to a chord, that line will bisect the chord.
Solved: #3 From The List Of Quadrilaterals, Select Two. Use The Venn Diagram To Compare And Contrast Them. List At Least Two Similarities And Two Differences For Each: Parallelogram Rectangle Rhombus Trapezoid
Euclid’s fifth law is more complicated than his others. A postulate is similar to a statement

If two lines are intersected by a transversal, the lines meet unless the alternate interior angles are equal.
If two lines are intersected by a transversal and alternate interior angles are equal, then the two lines are parallel.

Mathematical Musings: Classifying Quadrilaterals
Does Euclid have to prove the second statement separately or is it sufficient to appeal to the first statement?
Dr. “Say you have a statement like ‘$p$ means $q$,'” says Gordon. If that statement is true, then $p$ is sufficient for $q$ and $q$ is necessary for $p$. . “

Test this situation by trying some example statements (eg, “If you live in Baltimore, you live in Maryland.”).
Has All Right Angles And Has All Sides Congruent
During the 2008 presidential campaign, some worried whether Obama could still be a good president despite his lack of military experience. At the same time, General Wesley Clark pointed out that despite McCain’s impressive military experience, this experience did not necessarily prepare him well for the presidency.

Do Obama’s critics argue that military service is necessary to be a good president, or is it sufficient to be a good president?
Is Wesley Clark arguing that military service is neither necessary nor sufficient to be a good president?

Geometry 10.6 Quadrilateral Family.
Determine whether each of the following is a sufficient condition for the graph to be a parallelogram. You can think of these as “tests” to determine whether the shape is truly a parallelogram.
Both statements in the previous problem are correct. Write proof of each of them. (If you’re stuck on a resource,

; What do you have to show to show that something is a parallelogram? What tools do you have to show those things?)
Representing Rational Numbers With Python Fractions
Being hungry is a necessary condition to be a chef. Being oak is a sufficient condition for being oak. There are 22 Aces, 7 Oaks and 10 Chefs. 8 of the bracelets are not oak or kook. Now, suppose you pick a random egg and it turns out to be an oak, but what is the probability of an acorn?

Draw a set of quadrilaterals where the diagonals are perpendicular and where one diagonal bisects another (but not necessarily the other side). It may help to start with the diagonals and then draw the rest of the shape around them. What form does it always take?
Have you found a necessary condition for a quadrilateral to have this shape, a necessary condition, or both?

Quadrilaterals Homework 4 Worksheet
Does your theorem list already contain the terms you mentioned in the previous problem? If the class agrees, add them to your thesis list.
Suppose someone asks you to prove that if a quadrilateral is not a parallelogram, then at least one pair of opposite sides must not be congruent. Even if your thesis statement isn’t listed, explain why you don’t have to do much work.

In 9th grade, you learned about the built-in rule $a triangle b$, which takes the first number, adds the second number to it, adds the first number, then takes the whole answer and adds it. Multiplies the second number. For example, $7 triangle 2$ is 32.
Create A Venn Diagram Illustrating The Relationships Of The Following Geometric Figures Uall Quadrilateralspparallelogramsrrectanglesssquareskkitesttrapezoids
And in 9th grade, a mysterious man named John said: “To get an odd number for your answer from $a triangle b$, you need to enter odd numbers for $a$ and $b$. Did John get it right?

Has he found a necessary or sufficient condition for obtaining an odd number or is his condition both necessary and sufficient?
The 9th grade sign “&” means you take the first number and then add the product of the numbers. John said of this code: “To get an odd number for your answer from $a$&$b$, you must enter an odd number for $a$ and an even number for $b$.”
Naming And Describing Quadrilaterals In 3rd Grade
Numbers that can be expressed as a fraction (where the numerator and denominator are both integers and are not each equal to 0, or a recurring decimal (such as 4/3, .256256256…, and 8.000000…). Many
(such as square roots, cube roots and square roots) are not rational. Some roots of integers become integers like $sqrt[4]} = 2$. However, the roots of whole numbers do not work automatically
Venn diagram maker, free venn diagram, generate venn diagram, create a venn diagram, venn diagram generator free, editable venn diagram, fillable venn diagram, venn diagram software, online venn diagram creator, venn diagram design, venn diagram creator free, free venn diagram template
Thank you for visiting Venn Diagram Of Quadrilaterals. There are a lot of beautiful templates out there, but it can be easy to feel like a lot of the best cost a ridiculous amount of money, require special design. And if at this time you are looking for information and ideas regarding the Venn Diagram Of Quadrilaterals then, you are in the perfect place. Get this Venn Diagram Of Quadrilaterals for free here. We hope this post Venn Diagram Of Quadrilaterals inspired you and help you what you are looking for.
Venn Diagram Of Quadrilaterals was posted in December 27, 2022 at 8:55 am. If you wanna have it as yours, please click the Pictures and you will go to click right mouse then Save Image As and Click Save and download the Venn Diagram Of Quadrilaterals Picture.. Don’t forget to share this picture with others via Facebook, Twitter, Pinterest or other social medias! we do hope you'll get inspired by SampleTemplates123... Thanks again! If you have any DMCA issues on this post, please contact us!

