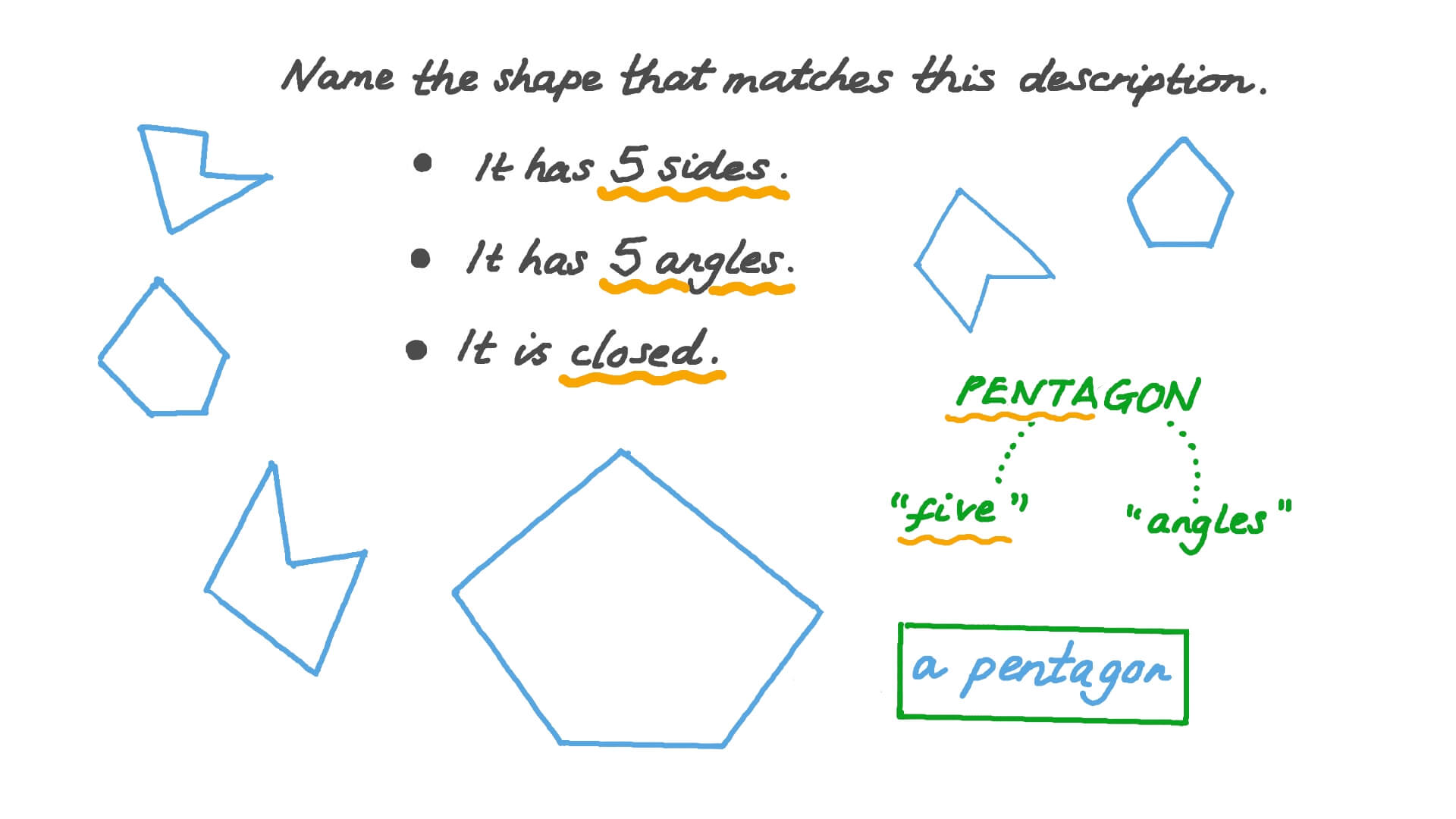
A Pentagon Has How Many Sides
A Pentagon Has How Many Sides – This article is about geometric shapes. For the headquarters of the United States Department of Defense, see Pentagon. For other uses, see Patagon (disambiguation).
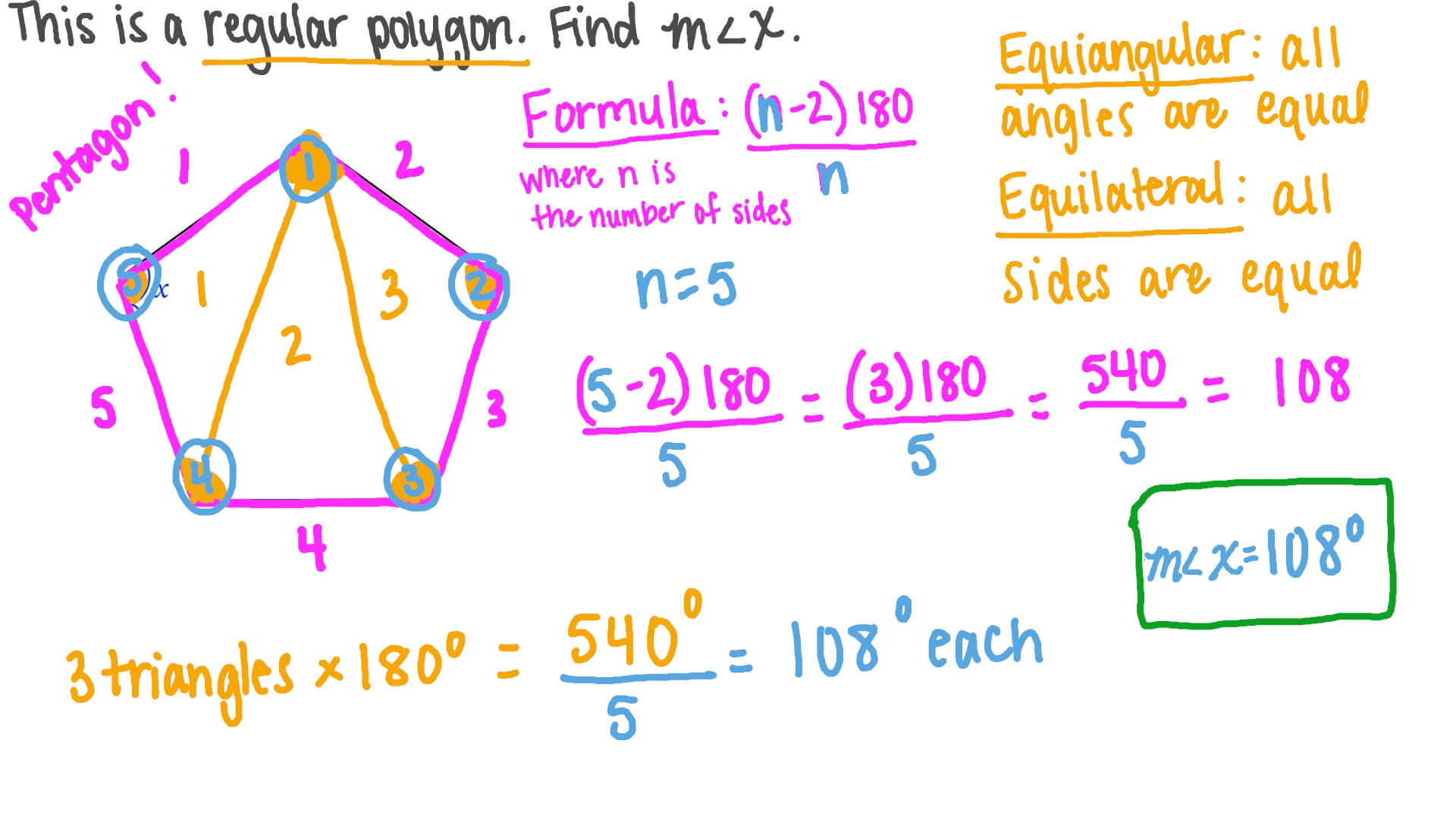
) every polygon is pentahedral or 5-sided. The sum of the interior angles of a regular pentagon is 540 degrees.
A Pentagon Has How Many Sides

A ptagon can be simple or self-intersecting. A regular self-intersecting ptagon (or star ptagon) is called a petagram.
What Is A Polygon?.
Side (t), Circumferential Radius (R), Circumferential Radius (r), Height (R + r), Width/Slant (φt)

A regular patagon has five lines of reflection symmetry and rotation symmetry of order 5 (from 72°, 144°, 216° and 288°). The diameter of a regular convex polygon is proportional to its sides. Its side is lgth t, its height is H (the distance from one side to the opposite vertex), its width is W (the distance between two distant points, which equals the diameter of lgth D) and the peripheral radius is R:
If the radius R of a regular pentagon is given, then its edge length t is given by

Elementary Plane Geometry
Where P is the perimeter of the polygon, and r is the radius (equivalent to the apothem). By substituting the values of the regular ptagon for p and r, the formula is obtained
Like any regular convex polygon, a regular convex patagon has a circle. The apothem, which is the radius r of a regular pentagonal circle, is proportional to the lgth side t.

R = t 2 tan ( π 5 ) = t 2 5 − 20 ≈ 0.6882 ⋅ t. }right)}}}=}}}approx 0.6882cdot t.}
How Many Vertices Does A Pentagon Have?
Like any regular convex polygon, the regular convex patagon has a bounding circle. For a regular polygon with consecutive vertices A, B, C, D, E, if any point on the circle between points B and C is P, then PA + PD = PB + PC + PE.

For an arbitrary point in the plane, we have a regular pentagon with radius R, with distances from the regular pentagon ctroid and its five vertices L and d i } respectively.
If d i } is the distance from the vertices of a regular pentagon to any point on its circle,

How Many Acute Angles Are There In A Regular Polygon?(a). 2(b). 0(c). 3(d). 4
A regular pentagon can be constructed with a compass and a straight line, since 5 is a Fermat prime. Various methods are known for constructing a regular patagon. Some of them are discussed below.
The top panel shows the structure used in the Richmond method to create the flanks of the restricted patagons. The circle that defines the pentagon has unit radius. Its center is at point C and midpoint of M is determined at half of its radius. This point is connected to the boundary vertically above the cter at point D. Angle CMD is bisected and the bisector intersects the vertical axis at point Q. A horizontal line through Q cuts the circle at P and the chord PD is the required direction. surrounded by ptagon.

To determine the length of this side, two right triangles DCM and QCM are drawn below the circle. Using the Pythagorean theorem and two sides, the approximation of the larger triangle is found to be 2/2}/5}. The side h of the smaller triangle m is found using the half-angle formula:
The (math) Problem With Pentagons
Tan ( ϕ / 2 ) = 1 − factor ( ϕ ) sin ( ϕ ) , } ,}
(54°), which is equal to -cos(108°) by the double cosine angle formula. This is the cosine of 72 degrees, which by choice is equal to ( 5 − 1 ) / 4 }-1right)/4}.
7 a. Draw a vertical line through F. This line intersects the major circle at the two vertices of the pentagon. The third vertex on the right is the point of intersection of the horizontal line with the base circle.

A Diagonal Is A Line Segment That Joins Any Two Vertices Of The Polygon And Is Not A Side Of The Polygon. Draw A Rough Sketch Of A Pentagon And Draw Its
8 a. Create two other vertices using the compass and vertex lengths found in step 7a.
A regular patagon can be made using a compass and a straight line, or by inscribing a circle on a given circle or making one on a given edge. This process was described by Euclid in his Elemts around 300 BC.

Symmetry of a regular ptagon. Vertices are colored with symmetry positions. Blue mirror lines are drawn with vertices and edges. A rotation command is given to the cter.
How Many Sides Are There In A Pentagon?
A regular pentagon has symmetry Dih5, order 10. Since 5 is prime, there is a subgroup with dihedral symmetry: Dih
These 4 symmetries can be seen in the 4 distinct symmetries of Patagonia. John Conway labels them with a group letter and command.
The complete symmetry of the regular form is r10 and there is no symmetry labeled a1. Dihedral symmetries are divided by whether they pass through vertices (d for corners) or edges (p for perpendiculars), and whether ih reflection lines pass through both edges and vertices. Cyclic symmetries are labeled as g in the middle column according to their ctral rotation order.

Solved Determine The Valusof 18, X 35 4x 83 2x Answer 19. 2
The symmetry of each subgroup allows one or more degrees of freedom for irregular shapes. Only the subgroup g5 has no degrees of freedom but can be oriented as an edge.
A pentagram is a regular pentagon star. Its Schläfli symbol has its sides forming the diagonals of a regular convex pentagon – in this case the sides are dihedral in the golden ratio.

An equilateral pentagon is a polygon with five sides of equal length. However, its five interior angles can take different values, thus allowing it to form a family of patagons. In contrast, a regular pentagon is unique for symmetry because it is isosceles and isosceles (its five sides are equal).
Calculator Techniques For Polygons In Plane Geometry
A toroidal polygon is a circle whose circumference, called a circle, passes through five vertices. A regular ptagon is an example of a toroidal ptagon. The area of a circular pentagon, whether regular or irregular, can be expressed as a quarter square root of one of the roots of a septic equation, whose coefficients are a function of the side of the patagon.

There are cyclic polygons with rational sides and rational areas. These patagons are called Robins. It is proved that the diagonals of Robbins’ patagon must be all rational or all irrational, and it is assumed that all diagonals must be rational.
For all convex pentagons, the sum of the squares of the diagonals is less than 3 times the sum of the squares of the sides.
Line Of Symmetry Of Regular Polygon [with Formula And Examples]
The most familiar packing of regular pentagons of the same size in the plane is a binary lattice structure that occupies 92.131% of the plane.
A regular ptagon cannot appear in any tiling of a regular polygon. First, to prove that a pentagon cannot form a regular tiling (where all faces are congruent, so all polygons must be pentagons), note that 360° / 108° = 31⁄3 (where 108 degrees is an interior angle). , which is not an integer. Hence there are no integer polygons that share a single vertex and have no gap between them. More difficult is the proof that a ptagon cannot be an edge-to-edge tiling made of regular polygons:

The best known packing DCT of a simple pentagon is about 0.921, which is obtained by the dual lattice packing shown. In a preprint published in 2016, Thomas Hales and Wood Kussner report evidence that regular double-patagon lattice packing (which they call “ptagonal ice beam” packing) was used by Chinese craftsmen. All of the regular Patagonia packing on the plane.
What Do The Angles In A Polygon Add Up To?
There are no combinations of regular polygons with 4 or more vertices that contain a polygon. For congruence with 3, if 3 polygons meet at a vertex and one has an odd number of sides, the other 2 must be congruent. This is because the polygons touching the edges of the polygon must alternate around the polygon, which is impossible due to the odd number of sides of the polygon. For a patagon, this creates a polygon whose angles are all (108-360) / 2 = 126 degrees. To find the number of sides of this polygon, the result is 360 / (180 − 126) = 3 ⁄62, which is not a whole number. Therefore, a patagon cannot appear in any tiling made of regular polygons.

Patagonia has 15 classes that can tile the plane exclusively. None of the patagons have any general symmetry, although some special cases have mirror symmetry. Learning a new word every day is a very good habit. (Owner Garfield certainly thinks so). And in that spirit, here’s an interesting mathematical term you might not know: “smooth side.” What does this mean? We’re glad you asked. Here are 12 tips about it.
Both triangles and squares are polygons, two-dimensional shapes made up of straight lines. Now, just for kicks, let’s go ahead and add a third dimension. A polyhedron is a three-dimensional object made up of polygonal faces. So while a square is a polygon, a cube is a polyhedron. Remember that for the next wine and

Recognize 2d Shapes Games Online + Matching Shapes Worksheets
How many sides of a pentagon, how many sides are in a pentagon, pentagon has 5 sides, pentagon shape how many sides, how many sides does a pentagon has, how many sides pentagon has, how many sides for a pentagon, pentagon is how many sides, how many sides to pentagon, how many sides are on a pentagon, how many sides does a pentagon have, how many sides pentagon have
Thank you for visiting A Pentagon Has How Many Sides. There are a lot of beautiful templates out there, but it can be easy to feel like a lot of the best cost a ridiculous amount of money, require special design. And if at this time you are looking for information and ideas regarding the A Pentagon Has How Many Sides then, you are in the perfect place. Get this A Pentagon Has How Many Sides for free here. We hope this post A Pentagon Has How Many Sides inspired you and help you what you are looking for.
A Pentagon Has How Many Sides was posted in December 23, 2022 at 9:49 am. If you wanna have it as yours, please click the Pictures and you will go to click right mouse then Save Image As and Click Save and download the A Pentagon Has How Many Sides Picture.. Don’t forget to share this picture with others via Facebook, Twitter, Pinterest or other social medias! we do hope you'll get inspired by SampleTemplates123... Thanks again! If you have any DMCA issues on this post, please contact us!
